USA Banner

Official US Government Icon

Official websites use .gov
A .gov website belongs to an official government organization in the United States.

Secure Site Icon

Secure .gov websites use HTTPS
A lock ( ) or https:// means you’ve safely connected to the .gov website. Share sensitive information only on official, secure websites.

U.S. Department of Transportation U.S. Department of Transportation Icon United States Department of Transportation United States Department of Transportation
FHWA Highway Safety Programs

Appendix. Alternative Calculations for Select Example Problems

A-3.2 Hand Calculated Example – Predicting Crash Frequency for Alternative Intersection Turn-lane Options at Four-Lane, Rural, Undivided Highways

Problem overview for section A-3.2 Hand Calculated Example – Predicting Crash Frequency for Alternative Intersection Turn-lane Options at Four-Lane, Rural, Undivided Highways.

Detailed Analysis:

This example demonstrates hand calculations for Problem 3.2 and Alternative #1. The full problem in Chapter 3 includes two alternative options. For this assessment, the analyst can use the SPF with CMF Adjustment method. This will provide the number of predicted crashes (estimated for a type of facility). The SPFs can be locally derived or the analyst can use the Highway Safety Manual (HSM) equations. If the analyst uses the safety performance functions (SPF) from the HSM, they should be calibrated for local conditions where possible. To perform a relative comparison between two options for the same location, this procedure can be used and a calibration value of 1.0 assumed. This hand-calculated example uses the rural undivided multilane predictive procedures located in Chapter 11 of the HSM.

STEP 1: Calculate the predicted average total crash frequency and fatal and injury frequency for the intersection and major road segment base conditions (NSPF).

Intersection Calculations (NSPF int):

From the HSM, use the SPF equation for intersection-related crashes at undivided rural multi-lane highways to calculate the average intersection total crash frequency. This base condition SPF applies to the existing configuration as well as the alternative.

Table calculates total crashes and fatal and injury crashes for intersections.

Segment Calculations (NSPF ru):

The HSM equation for undivided roadway segments can be used to calculate the average segment crash frequency. This SPF applies to the existing design as well as the alternative intersection configuration. Recall that each approach segment is 0.19 miles for a total study length of 0.38 miles.

Table calculates total crashes and fatal and injury crashes for segments.

STEP 2: Calculate the predicted average crash frequency for the segment and intersection unique design conditions (Npredicted).

The predicted average crash frequency (Npredicted) for each option can be calculated using the following equation (HSM Equation 11-1, p. 11-2):

Npredicted = Nspf × (CMF1x × CMF2x ×...× CMFyx ) × Cx

Where: CMF = crash modification factor/function and C = calibration factor for SPF

[Notice that any countermeasure that matches base conditions will have a CMF value of 1.0 and does not change the value of Npredicted.]

Predicted Average Crash Frequency (Nint) for Intersections

The intersection-related CMFs that do not match base conditions are next included in the calculations. For this example, a calibration factor of 1.0 is assumed (assuming the HSM predictive equations are representative of local conditions). The required CMFs are:

Table describes the following equations: Left-turn lane crash modification factor for total crashes equals 0.52. (Use HSM Table 11-22, p. 11-34 for left-turn lanes (Alternative)). Left-turn lane crash modification factor for fatal and injury crashes equals 0.42. (Use HSM Table 11-22, p. 11-34 for left-turn lanes (Alternative))

The predicted number of intersection-related crashes is then calculated by multiplying the CMFs and the calibration factor times the appropriate Nspf int value.

Calculations to obtain the predicted number of intersection-related crashes.

Segment Predicted Average Crash Frequency

The segment-related CMFs that do not match base conditions are next included in the calculations. These are the required CMFs:

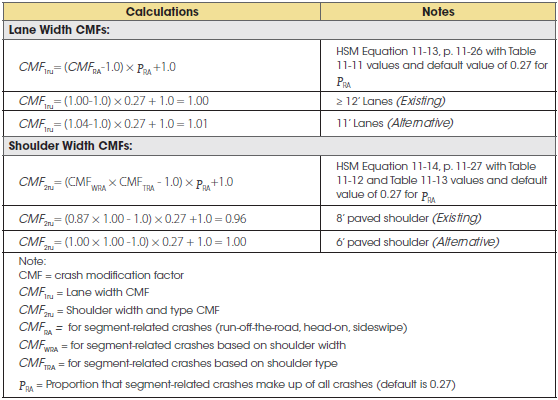
Lane and shoulder width calculations for segments that do not match base conditions.

The predicted number of segment-related crashes is then calculated by multiplying the CMFs and the calibration factor times the appropriate Nspf ru value.

Calculations to obtain the predicted number of segment -related crashes.

STEP 3: Add the intersection and segment crashes per year to calculate the total and FI predicted crashes (N(predicted (Total)) and (N(predicted (FI)).

Alternative Total Crashes per Year Fatal and Injury Crashes per Year
Intersection Crashes Segment Crashes Predicted Crashes Intersection Crashes Segment Crashes Predicted Crashes
Existing 12.8 4.31 17.11
(say 18)		 7.94 2.36 10.30
(say 11)
Alternative #1 6.66 4.53 11.19
(say 12)		 3.33 2.48 5.81
(say 6)
Difference 6.14 -0.22 5.92
(say 6)		 4.61 -0.12 4.49
(say 5)
Percent Reduction 48.0% -5.1% 34.60%
(say 34%)		 58.1% -5.1% 43.6%
(say 43%)

 

Manual calculations are shown only for total crashes. Calculations for fatal and injury (FI) and property damage only (PDO) crashes are calculated in a similar manner. The hand calculations include rounded values. The self-calculating spreadsheets do not truncate the numbers and so rounding errors are not included. Consequently, the hand calculated results may have minor differences than the spreadsheet calculated values.

A-3.4 Hand Calculated Example – Calculating Expected Crashes for Urban Freeway Ramps

Problem overview for section A-3.4 hand calculated example – calculating expected crashes for urban freeway ramps.

Detailed Analysis:

This example demonstrates hand calculations for Problem 3.4. The full problem in Chapter 3 includes calculations that demonstrate the use of the free ISATe self-calculating "Smart Spreadsheet." For this assessment, the analyst can use the SPF with CMF Weighted with Observed Crashes method. This assessment is for a specific location with a known crash history, so the expected number of crashes can be calculated. Because the ramp's cross-sectional characteristics are consistent along its entire length, the ramp can be modeled as one segment.

The following steps summarize the process for performing hand calculations to evaluate the expected crashes.

STEP 1: Calculate the predicted average crash frequency, Nspf.

Multiple-vehicle crashes:

The HSM equations for multiple-vehicle FI and PDO crashes at freeway ramps are summarized as follows:

The HSM equations for multiple-vehicle FI and PDO crashes at freeway ramps.

Single-vehicle crashes:

The HSM equations for single-vehicle FI and PDO crashes at freeway ramps are summarized as follows:

The HSM equations for single-vehicle FI and PDO crashes at freeway ramps.

STEP 2: Apply the appropriate CMFs and calculate the predicted average crash frequency (Npredicted)

Calculate CMF values for any conditions that differ from the base conditions.

CMF for Horizontal Curve:

The horizontal curve CMF requires an average entry speed (vent,i), the radius for the entry curve (Ri), the proportion of the segment length with the curve (Pc,i), and the number of horizontal curves in the segment (m). To calculate this CMF value, the limited curve speed (curve with the sharpest radius) must first be identified.

The equations in this table describe ho to obtain the CMF for a horizontal curve.

Table shows how to calculate the CMFs for a horizontal curve based on HSM equation 19-33.

CMF for Lane Width:

Table shows how to calculate the CMFs for lane width.

CMF for Shoulder Width:

Table shows how to calculate the CMFs for right shoulder width.



Table shows how to calculate the CMFs for the left shoulder width.

CMF for Roadside Barrier:

Table shows how to calculate the CMFs for a right shoulder barrier.



Table shows how to calculate the CMFs for a left side barrier.

STEP 3: Calculate the predicted average crash frequency for the segment under unique design conditions (Npredicted)

Calculation to find the predicted average crash frequency for the segment.

STEP 4: Calculate the expected crashes.

The next step is to evaluate the expected number of total crashes.

Calculations to evaluate the expected number of total crashes.

Summary table:

Calculations to evaluate total crashes, all severities.

A-4.1 Hand Calculated Example – Predicting Crashes for a New Urban Multilane Arterial

Problem overview for section A-4.1 Hand Calculated Example – Predicting Crashes for a New Urban Multilane Arterial.

Detailed Analysis:

The urban multilane predictive method is located in Chapter 12 of the HSM. The following steps summarize the manual calculation for the proposed configurations as described in Problem 4.1.

STEP 1: Calculate the predicted average crash frequency and fatal and injury frequency for the proposed road segment.

Segment Calculations (NSPF RS):

Use the SPF equation in the HSM for segment-related crashes at divided urban multi-lane arterials to calculate crash frequency:

Equations for calculating crash frequency for multiple-vehicle non-driveway collisions.



Equations for calculating crash frequency for single-vehicle related crashes and multiple-vehicle driveway-related collisions.

STEP 2: Calculate the Crash Modification Factors:

Equations for calculating CMFs for median width, lighting, and automated speed enforcement.

STEP 3: Calculate the predicted average crash frequency for the design conditions (Npredicted).

The predicted average crash frequency (Npredicted) can be calculated using the following equations:

Nbr = Nspf × (CMF1r × CMF2r × CMF3r × CMF4r × CMF5r )

 

Npredicted = (Nbr + Npedr + Nbiker) × Cr

Calculations for the predicted average crash frequency for the design conditions.

Manual calculations are shown only for total crashes. Calculations for FI and PDO crashes are calculated in a similar manner. The hand calculations include rounded values. The self-calculating spreadsheets do not truncate the numbers and so rounding errors are not included. Consequently, the hand calculated results may have minor differences than the spreadsheet calculated values.

A-4.3 Hand Calculated Example – Documenting a Design Decision for a Sharp Horizontal Curve on a Rural Two-Lane Highway

Problem over view for section A-4.3 Hand Calculated Example – Documenting a Design Decision for a Sharp Horizontal Curve on a Rural Two-Lane Highway

Detailed Analysis:

The predictive methods for rural two-lane highways and curved roadway segments are located in Chapter 10 of the HSM. The following steps summarize the process for performing hand calculations to evaluate safety treatments that can be included in the preliminary or final design phases.

STEP 1: Calculate the average crash frequency for the rural two-lane road segments considering base conditions (NSPF). This value represents the number of crashes for any rural two-lane highway with a similar traffic volume and only base conditions.

Segment Calculations (NSPF RS):

Use the SPF equation from the HSM for rural two-lane undivided roadway segments to calculate the average segment crash frequency:

Equations for calculating the number of total crashes for rural two-lane undivided roadway segments.

STEP 2: Calculate predicted average crash frequency for the segment under unique design conditions (Npredicted). This value represents the number of crashes for any rural two-lane highway with a similar traffic volume and similar geometric characteristics.

To calculate the estimated CMF due to decreasing the curve radii, the designer must first estimate the CMF of installing a curve compared to a base condition of a straight section of road.

Equations for calculating the CMF of installing a curve compared to a base condition of a straight section of road.

Next calculate the CMF for the new curve using the same method.

Equations for calculating the CMF of the new curve.

The predicted average crash frequency (Npredicted) can then be calculated using the following equation:

Equations for calculating the predicted average crash frequency for the new curve.